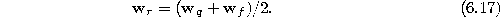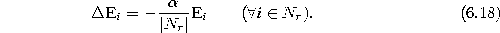Next: Growing Grid
Up: Soft Competitive Learning with
Previous: Self-organizing Feature Map
This model (Fritzke, 1994a) is rather
similar to the growing neural gas model

. The main difference is that the network
topology is constrained to consist of k-dimensional simplices
whereby k is some positive integer chosen in advance. The basic
building block and also the initial configuration of each network is a
k-dimensional simplex. This is, e.g., a line for k=1, a triangle for
k=2, and a tetrahedron for k=3.
For a given network configuration a number of adaptation steps are used to
update the reference vectors of the nodes and to gather local error
information at each node.
This error information is used to decide
where to insert new nodes. A new node is always inserted by splitting the
longest edge emanating from the node q with maximum accumulated error. In
doing this, additional edges are inserted such that the resulting structure
consists exclusively of k-dimensional simplices again.
The growing cell structures learning procedure is described in the following:
- 1.
- Choose a network dimensionality k.
Initialize the set 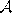 to contain k+1 units
to contain k+1 units 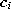

with reference vectors 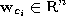 chosen randomly according to
chosen randomly according to
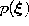 .
.
Initialize the connection set  ,
, 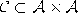 such that
each unit is connected to each other unit, i.e., such that the network has the topology of a k-dimensional simplex.
such that
each unit is connected to each other unit, i.e., such that the network has the topology of a k-dimensional simplex.
- 2.
- Generate at random an input signal
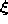 according to
according to 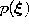 .
.
- 3.
- Determine the winner s:
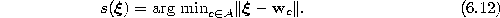
- 4.
- Add the squared distancebetween the input signal and the winner unit s to a local
error variable
 :
:
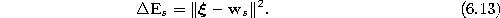
- 5.
- Adapt the reference vectors of s and its direct
topological neighbors towards
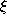 by fractions
by fractions
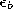 and
and 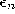 , respectively, of the total distance:
, respectively, of the total distance:
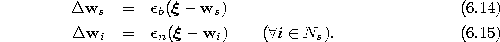
Thereby, we denote with 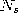 the set of direct topological neighbors of s.
the set of direct topological neighbors of s.
- 6.
- If the number of input signals generated so far is an integer multiple
of a parameter
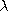 , insert a new unit as follows:
, insert a new unit as follows:

- Determine the unit q with the maximum accumulated error:
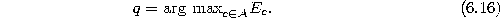

- Insert a new unit r by splitting the longest edge emanating from q,
say an edge leading to a unit f. Insert the connections (q,r) and
(r,f) and remove the original connection (q,f). To re-build the
structure such that it again consists only of k-dimensional simplices, the
new unit r is also connected with all common neighbors of q and f,
i.e., with all units in the set
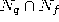 .
.

-
Interpolate the reference vector of r from the reference vectors of q and f:
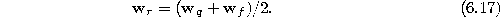

- Decrease
the error
variables of all neighbors of r by a fraction which depends on the number of neighbors of r:
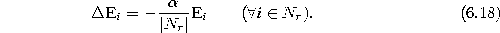

-
Set the error variable of the new unit r to the mean value of its
neighbors:

- 7.
- Decrease the error variables of all units:

- 8.
- If a stopping criterion (e.g., net size or some performance measure) is
not yet fulfilled continue with step 2.
Figure 6.3 shows some stages of a simulation for a simple ring-shaped data distribution. Figure 6.4 displays the final results after 40000 adaptation steps for three other distribution.
The parameters used in both simulations were: 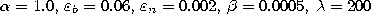 .
.
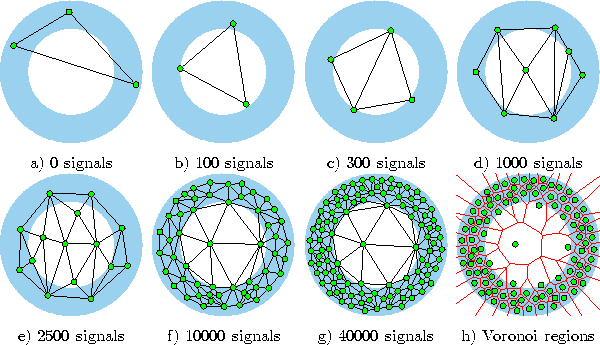
Figure 6.3: Growing cell structures simulation sequence for a ring-shaped uniform probability distribution. a) Initial state. b-f) Intermediate states. g) Final state. h) Voronoi tessellation corresponding to the final state. Per construction the network structure always consists of hypertetrahedrons (triangles in this case).
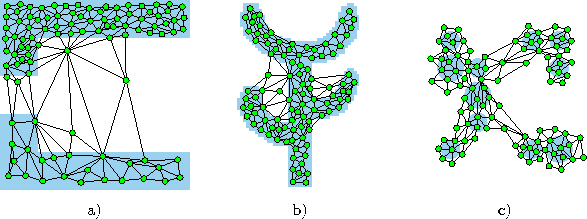
Figure: Growing cell structures simulation results after 40000 input signals for three different probability distributions (described in the caption of figure 4.4).




Next: Growing Grid
Up: Soft Competitive Learning with
Previous: Self-organizing Feature Map
Bernd Fritzke
Sat Apr 5 18:17:58 MET DST 1997
![]() to contain k+1 units
to contain k+1 units ![]()
![]()
![]() chosen randomly according to
chosen randomly according to
![]() .
.
![]() ,
, ![]() such that
each unit is connected to each other unit, i.e., such that the network has the topology of a k-dimensional simplex.
such that
each unit is connected to each other unit, i.e., such that the network has the topology of a k-dimensional simplex.

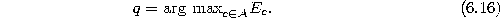

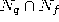 .
.