Neural Gas plus Competitive Hebbian Learning

 

• Common Properties and Notational Conventions
• Java implementation
  

This method (Martinetz and Schulten, 1991, 1994) is a straight-forward superposition of neural gas and competitive Hebbian learning. It is sometimes denoted as ``topology-representing networks'' (Martinetz and Schulten, 1994). This term, however, is rather general and would apply also to the growing neural gas model described later.

At each adaptation step a connection between the winner and the second-nearest unit is created (this is competitive Hebbian learning). Since the reference vectors are adapted according to the neural gas method a mechanism is needed to remove edges which are not valid anymore. This is done by a local edge aging mechanism. The complete neural gas with competitive Hebbian learning algorithm is the following:

1. Initialize the set to contain N units
   
   with reference vectors chosen randomly according to .

   Initialize the connection set , , to the empty set:
   
   

   Initialize the time parameter t:
   
   

2. Generate at random an input signal according to .
3. Order all elements of according to their distance to , i.e., find the sequence of indices such that is the reference vector closest to , is the reference vector second-closest to and is the reference vector such that k vectors exist with . Following Martinetz et al. (1993) we denote with the number k associated with .
4. Adapt the reference vectors according to
   
   with the following time-dependencies:
   
   
   
   
   
   
5. If it does not exist already, create a connection between and :
   
   Set the age of the connection between and to zero (``refresh'' the edge):
   
   
6. Increment the age of all edges emanating from :
   
   Thereby, is the set of direct topological neighbors of c (see equation 2.5).
7. Remove edges with an age larger than the maximal age T(t) whereby
   
   
8. Increase the time parameter t:
   
   
9. If continue with step 2.

For the time-dependent parameters suitable initial values and final values have to be chosen.

Figure 5.5 shows some stages of a simulation for a simple ring-shaped data distribution. Figure 5.6 displays the final results after 40000 adaptation steps for three other distribution. Following Martinetz et al. (1993) we used the following parameters: . The network size N was set to 100.

 
Figure 5.5:   Neural gas with competitive Hebbian learning simulation sequence for a ring-shaped uniform probability distribution. a) Initial state. b-f) Intermediate states. g) Final state. h) Voronoi tessellation corresponding to the final state. The centers move according to the neural gas algorithm. Additionally, however, edges are created by competitive Hebbian learning and removed if they are not ``refreshed'' for a while.

 
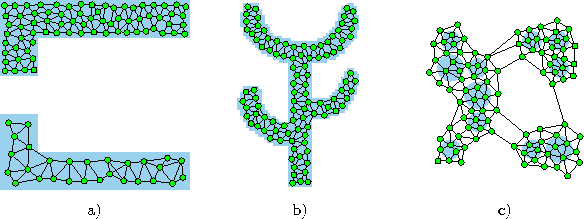
Figure:   Neural gas with competitive Hebbian learning simulation results after 40000 input signals for three different probability distributions (described in the caption of figure 4.4).